Primena i implementacija algoritma za detekciju zenica baziranog na obradi slike

Autori

Anja Kovačev, učenica III razreda Tehničke škole u Kikindi

Lenka Milojčević, učenica II razreda Gimnazije u Kraljevu

Mentori

Milomir Stefanović, diplomirani inženjer elektrotehnike i računarstva, PFE

Pavle Pađin, Elektrotehnički fakulteta u Beogradu

Apstrakt

Cilj ovog rada je dizajn hardverskog sistema i implementacija softverskog rešenja za detekciju zenice u svrhu njenog praćenja. Primena detekcije zenice u okviru ovog istraživanja ogleda se u upravljanju pozicijom kursora. Za dobijanje informacija o koordinatama centra zenice korišćena je web kamera. Na snimku sa kamere izvršena je segmentacija zenice, nakon čega je, primenom Hafove transformacije, određeni njen centar i poluprečnik. Primenom polinomialne regresije 3. reda izvršena je transformacija koordinata zenice u koordinate kursora. Posmatrane su greške predikcije pozicije kursora u odnosu na ciljanu poziciju. Dobijeni rezultati ukazuju na prosečno odstupanje procene od 121,6 piksela, što nije zadovoljavajuće za primenu u realnom vremenu, poput upravljanja kursorom. Za unapređenje sistema i ostvarenje praktične primene, neophodno je proširiti skup podataka većim brojem snimaka, dodati IR diode na 3D nosač web kamere i primeniti crveni i plavi filter, što bi doprinelo značajnom smanjenju greške estimacije.

Ključne reči: obrada slike, videookulografija, algoritam za detekciju zenice, polinomijalna regresija

Abstract

The aim of this work is the design of a hardware system and the implementation of a software solution for pupil detection with the purpose of tracking it. The application of pupil detection in this research is focused on controlling the position of the cursor. A webcam was used to obtain information about the coordinates of the pupil center. In the camera footage, the pupil was segmented, after which its center and radius were determined using the Hough transform. By applying third-order polynomial regression, the transformation of pupil coordinates into cursor coordinates was performed. The errors in cursor position prediction relative to the target position were analyzed. The obtained results indicate an average estimation deviation of 121.6 pixels, which is not satisfactory for real-time applications such as cursor control. To improve the system and enable practical implementation, it is necessary to expand the dataset with a larger number of recordings, add IR LEDs to the 3D webcam mount, and apply red and blue filters to the webcam. These measures would significantly reduce the estimation error.

Keywords: image processing, video oculography, pupil detection algorithm, polynomial regression

1. Uvod

Život u današnjem društvu ima mnogo prednosti u svakom pogledu. Tehnologija napreduje iz dana u dan. Taj brz razvoj zahteva velike potrebe koje ne mogu svi ljudi da ispune. Uočivši potrebe osoba sa invaliditetom za komunikacijom, igranjem video igara, korišćenjem računara i kretanjem, odlučeno je da se ovaj rad posveti razvoju sistema koji bi mogao da im pruži podršku. Za rešavanje ovakvih problema često se koriste metode elektrookulografja i videookulografija. Napretkom tehnologije, VOG (videookulografija) je zamenila EOG (elektrookulografiju). Videookulografija je metoda u kojoj se pomoću kamere prate pokreti oka, tj. zenice. U ovom radu proučavan je 2D VOG sistem, tj. pokreti zenice na dve ose – horizontalna osa na kojoj se detektuju pokreti na levo i desno, i vertikalna osa na kojoj je prate pogled na gore i dole.

2D VOG se smatra jednom od najpouzdanijih modaliteta za praćenje pokreta očiju i nalazi široku primenu. Primenjuje se u oftalmologiji za proučavanje patoloških stanja, poput nistagmusa, koji se karakteriše ritmičkim, nevoljnim pokretima očnih jabučica. VOG sistem koriste osobe sa kvadriplegijom i oštećenjem motornih neurona kao sredstvo za komunikaciju i kretanje, odnosno za upravljanje tastaturom i invalidskim kolicima pomoću pokreta očiju. Takođe, nalazi primenu u industriji za analizu reakcija korisnika. Ova tehnologija se koristi i za posmatranje ponašanja vozača tokom vožnje, u vojne svrhe i slično. Cilj ovog rada je konstruisanje jednostavnog 2D VOG koji se može koristiti za praćenje zenice.

Navedeni referentni radovi^{1 2 3} koriste metodu tamne zenice, što znači da je zenica najtamniji objekat na slici. U referentnom radu ¹ za akviziciju slike korišćena je IR kamera čije su LED diode (za vidljivi spektar boja) zamenili IR LED diodama kako bi sve dužice, nezavisno od njihove boje, bile svetle. Algoritam referenthih radova ^{1 2 3} (uz manje izmene) sastoji se iz akvizicije slike, kalibracije sistema, detekcije zenice, mapiranja slike oka u odnosu na postavku na ekranu, selekciju objekata i stabilizaciju kursora (odnosi se na radove koji za cilj imaju kontrolu kursora). Kako bi procedura binarizacije bila uspešna, potrebna je funkcija mapiranja koja mapira sliku oka i sliku ekrana. Proizvod ove funkcije su centar zenice oka i koeficienti mapiranja potrebni za ranije navedenu binarizaciju. Mapiranje se postiže posmatranjem slike oka u ondosu na sliku ekrana izdeljenu na 9 delova. Zbog nelinearnosti sistema, za mapiranje koristi se bikvadratna funkcija koja kompezuje pomenutu nelinearnost. Referentni rad ¹ navodi da, za veću tačnost sistema, potrebno je uvesti stopu mapiranja između slike oka i ekrana. Ta stopa mapiranja dalje daje indikator koji karakteriše preciznost sistema. Indikator se dobija procenjivanjem stope mapiranja tokom kalibracije, koja se zbog nelinearnost sistema mora računati posebno za svih 9 delova ekrana. U sledećem koraku se računa srednja vrednost za stopu mapiranja kako bi ista mogla da bude procenjena zbog računanja indikatora. Potom, traže se prečnik i centar kruga. Više radova ¹ se zasniva na binarizaciji slike implementirane korišćenjem različitih metoda za određivanje paraga. Neke od njih su - globalni ili lokalni adaptivni prag. Od 6 korišćenih PDA algoritama, većina koristi novu metodu za binarizaciju slike, implementiranu na adaptivnoj kvantitativnoj segmentaciji. U referentnim radovima postoje primeri uklanjanja šumova tehnikom bazirane na maksimalno određenom prostoru u praćenju rekonstrukcije zenice. Svi radovi uključuju Hafovu transformaciju kruga i morfološke operacije (erozija i dilatacija). Rad ¹ za detekciju ivica kruga koristi derivat drugog reda rezultujuće slike, što je postignuto Laplacom od Gausovog filtera. Poslednji korak je određivanje centra zenice algoritnom centroidne metode čime je uspešno detektovana zenica.

3. Aparatura i metode

3.1 Aparatura

Na Slici 1 prikazana je korišćena eksperimentalna aparatura, sastavljena od veb kamere, nosača kamere i 3D štampanih naočara. Veb kamera, kojoj je uklonjen infracrveni (IR) filter, korišćena je za praćenje zenice oka. Uklanjanje IR filtera omogućava pouzdanije detektovanje zenice nezavisno od boje dužice. Model nosača kamere izrađen je u CAD softverskom paketu i potom 3D odštampan. Ovaj držač ima sledeće opcije za podešavanje položaja:

1. Podešavanje rastojanja od oka – ostvaruje se pomeranjem šarke duz x na koju je veb kamera pričvršćena, čime se kamera može približiti ili udaljiti u skladu sa potrebama korisnika.

2. Podešavanje visine – omogućeno je pomeranjem veb kamere duž y ose pomoću klizača.

Web kamera ja pričvršćena na naočare gde su postavljene i LE diode kako bi osvetljenje slike bilo konstantno.

3.2. Metode

Projekst se sastoji iz dve faze:

1. Obrada slike, odnosno okvira snimka u realnom vremenu;
2. Obrade podataka, odnosno filtriranje podataka i kalibracija.

3.2.1. Obrada slike

Kako bi zenica bila detektovana neophodno je pronaći koordinate centra zenice. Obrađivanjem slike, tačnije svakog frejma snimka u realnom vremenu, dobijaju se podaci o koordinatama centra zenice. Proces obrade slike se sastoji iz sledećih koraka:

1. Prebacivanje slike iz RGB u grayscale prostor boja
2. Zamućivanje slike
3. Binarizacije slike
4. Morfoloških operacija
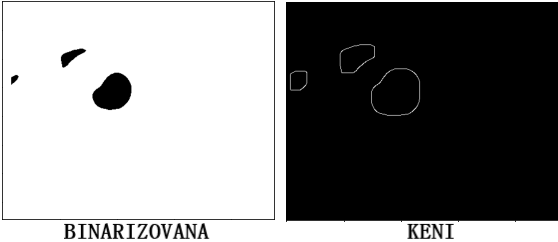
5. Detekcije ivica pomoću Keni algoritma
6. Detekcije krugova, odnosno zenice na slici pomoću Hafove transformacije

3.2.1.1. Prebacivanje slike iz RGB u grayscale prostor boja

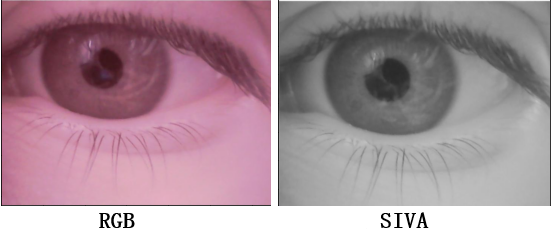
Slika u RGB spektru ima više informacija koje nam nisu potrebne, takođe slika u RGB spektru je kompleksnija za obradu pa iz tih razloga biramo greyscale ⁴. Konvertovanjem RGB vrednosti piksela slike koje zauzimaju 24 bita u grayscale prostor boja koji zauzima 8 bita memorije dobija se slika u monohromatkskom sistemu boja. Na slici 2 može se videti kako slika izgleda u RGB prostoru i njen sivi ekvivalent.

3.2.1.2. Zamućivanje

Kako bi binarizacija slike bila efikasnija, neophodno je prethodno zamućivanje slike korišćenjem Gausovog filtera, čime se smanjuje količina detalja i šuma na posmatranoj slici. Gausov filter predstavlja niskopropusni filter koji omogućava zadržavanje niskofrekventnih komponenti slike, dok visoke frekvencije, koje odgovaraju sitnim detaljima i šumu, bivaju potisnute.

Filtriranje se vrši konvolucijom svakog piksela slike sa Gausovim kernelom. Da bi konvolucija bila pravilno definisana, dimenzije kernela moraju biti pozitivne i neparne.

Proces konvolucije se odvija tako što se početni piksel slike množi sa centralnim elementom kernela, dok se preostali elementi kernela množe sa odgovarajućim preklopljenim pikselima slike. Dobijeni proizvodi se sabiraju i rezultujuća suma postaje nova vrednost posmatranog piksela. Nakon toga, kernel se pomera za jedan piksel udesno, a postupak se ponavlja sve do obrade poslednjeg piksela slike.

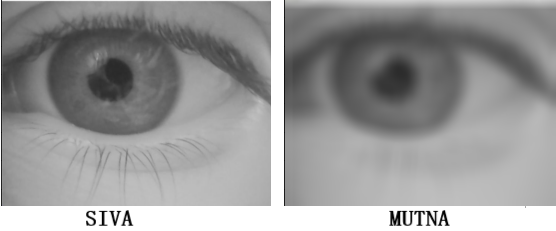
Ovim procesom se dobija filtrirana, odnosno u ovom slučaju zamućena slika. Na Slici 3 prikazana je slika pre i posle primene Gausovog zamućivanja.

3.2.1.3. Binarizacija

Binarizacija, kao pripremna faza za proces segmentacije, ima za cilj da svakom pikselu slike dodeli jednu od dve moguće oznake: 0 (crno) ili 1 (belo). Ovaj postupak se zasniva na poređenju intenziteta piksela sa unapred definisanom pragu, čime se slika iz sivog spektra transformiše u binarnu formu.

Konkretno, svaki piksel dobija vrednost 0 ili 255, u zavisnosti od toga da li je njegova originalna vrednost manja ili veća od zadatog praga. Kako bi prag bio adaptivan u odnosu na konkretne karakteristike slike, on se definiše tako da predstavlja vrednost ispod koje se nalazi 17,5% piksela cele slike.

Rezultat primene ovog postupka jeste binarna (crno-bela) slika, nad kojom se dalje sprovodi proces segmentacije, tj. izdvajanje zenice.

3.2.1.4. Morfološke operacije

Kako bi bile otklonjene ,,rupe" i suvišni objekti na slici koji nisu bitni za dalju obradu slike koriste se morfološke operacije, erozija i dilatacija.

3.2.1.4.1. Erozija

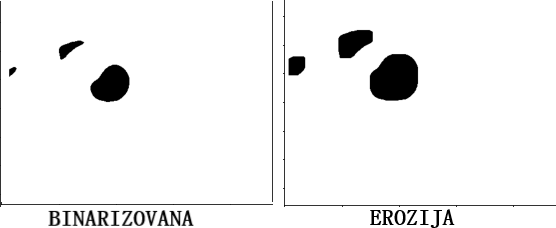
Erozija predstavlja postupak ,,uklanjanja" suvišnih objekata. Ona funkcioniše jednostavnim principom prolaska maske kroz sliku. Maska predstavlja kvadratnu matricu sa neparnim brojem dimenzije koja je ispunjena jedinicama. Polazeći od prvog piksela slike, koji se poklapa sa centrom maske, proverava se da li se maska poklapa sa svim njoj odgovarajućim pikselima slike. Ukoliko se dogodi da postoji barem jedno nepodudaranje, piksel slike koji se poklapa sa centrom maske dobiće vrednost 0, tj. postaće crni piksel. Nakon završetka ovog procesa, maska se pomera za jedan piksel udesno i tako se nastavlja postupak sve do kraja slike.

3.2.1.4.2. Dilatacija

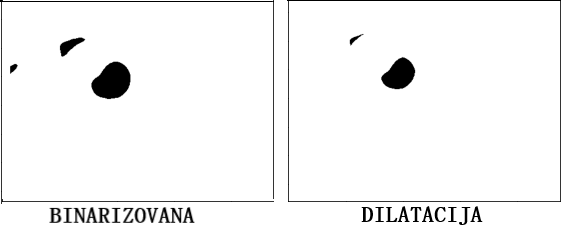
Dilatacija predstavlja postupak proširenja objekta sa ciljem izvršavanja proširenja njegovih ivica. Korišćenjem već konstruisane maske prolazi se kroz sliku, polazeći od prvog piksela slike, koji se poklapa sa centrom maske, proverava se da li postoji poklapanja između maske i njoj odgovarajućih piksela slike. Ukoliko se dogodi da postoji barem jedno poklapanje, piksel slike koji se poklapa sa centrom maske dobiće vrednost 1, tj. postaće beo piksel. Nakon završetka ovog procesa, maska se pomera za jedan piksel udesno i tako se nastavlja postupak sve do kraja slike.

3.2.1.5. Detekcija ivica

Za detekciju ivica zenice korišćen je Keni(eng. Canny) algoritam. Keni algoritam je jedan od najboljih metoda sa preciznu i pouzdanu detekciju ivica. Proces detekcije je sledeći⁵:

1. Zamućivanje - Svaka slika na sebi ima neke šumove koje je potrebno odbaciti kako ne bi pogrešno bili detektovani kao ivice. U te svrhe se koristi prethodno opisan Gausov filter.

2. Pronalaženje gradijenta intenziteta - Cilj Keni algoritma je da nađe ivice gde je razlika između piksela u sivom prostoru boja najveća, a to se može postići pronalaženjem gradijenta slike. Korišćenjem Sobelovog operatora određuje se gradijent svakog piksela.

3. Potiskivanje lokalnih ne-maksimuma - U ovoj fazi se ,,zamućene’’ ivice pretvaraju u ivice ,,od interesa’’ tako što se zadržavaju svi pikseli čiji je gradijent maksimalan u odnosu na gradijente osam piksela sa kojim se graniči, u suprotnom, vrednost piksela će biti eliminisana. Pikseli koji su maksimalni u svom ,,susedstvu’’ se označavaju belim ivicama.

4. Poređenje sa pragom – Da bi se postigao nizak procenat lažnih, a visok procenat pravih detekcija, definišu se dva praga: viši prag $T_H$ i niži prag $T_L$. Viši prag $T_H$ postavlja se tako da većina piksela koji ne pripadaju ivicama ima magnitudu gradijenta manju od ove vrednosti, odnosno, sve ivice sa magnitudom većom od $T_H$ smatraju se jakim ivicama. Niži prag $T_L$ postavlja se tako da većina piksela koji pripadaju ivicama koje želimo da detektujemo imaju magnitudu gradijenta veću od ove vrednosti, odnosno, sve ivice sa magnitudom manjom od $T_L$ se eliminišu. Na kraju ostaju sve ivice čije vrednosti leže između $T_L$ i $T_H$. Na ovaj način se formira mapa jakih i slabih (potencijalnih) ivica.

5. Detektovanja ivica - Prolaženjem kroz mapu slabih ivica, svi pikseli koji u svom susedstvu imaju barem jednu jaku ivicu proglašavaju se ivičnim pikselima. Ova iteracija se ponavlja sve dok broj ivica ne postane konstantan tokom cele iteracije.

Na slici 7 levo prikazan je binarizovani okvir snimka u realnom vremenu, odnosno okvir koji obrađuje Canny algoritam, dok je na slici 7 desno prikazan okvir istog snimka nakon izvršene detekcije ivica.

3.2.1.6. Hafova transformacija za krug

Hafova transformacija za krug (CHT)^{6 7} je metoda za detekciju krugova na slici. U ovom radu CHT se koristi kako bi se istakla zenica kao najjasniji detektovani krug.

Hafova transformacija za detekciju krugova zasniva se na principima transformacije za pravu (LHT). LHT se zasniva na sledećem:

Jednačina prave data je kao

$$ y_1 = a \cdot x_1 + b, $$

gde su:

• $y_1$ zavisna promenljiva,
• $x_1$ nezavisna promenljiva,
• $a, b$ parametri prave.

Ova jednačina se posmatra iz drugačijeg ugla, pri čemu parametri $a$ i $b$ postaju nezavisna i zavisna promenljiva, dok $x_1$ i $y_1$ prelaze u uloge parametara. Na taj način dobija se formula:

$$ b = -x_1 \cdot a + y_1. $$

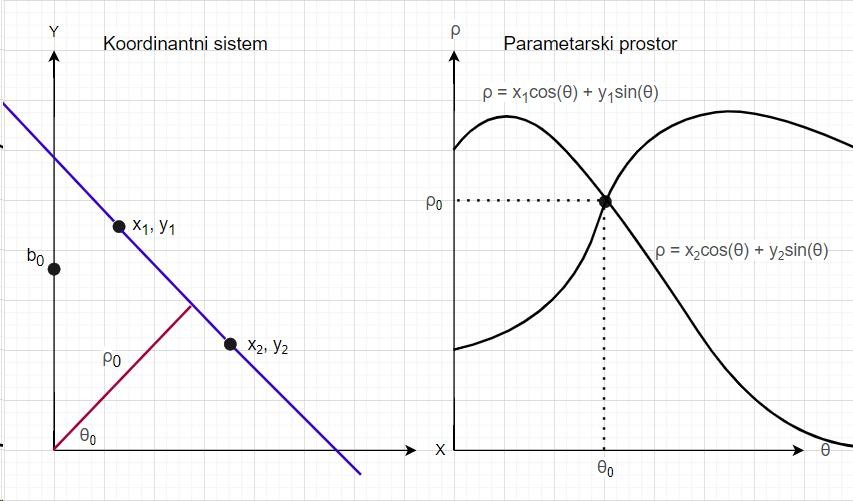
Ovim postupkom vidi se ideja Hafove transformacije, a to je da svaka tačka u Dekartovom koordinantnom sistemu predstavlja pravu u parametarskom prostoru slika 8.

Problem nastaje kada se dobije vertikalna linija, jer kod takvih parametar a teži beskonačnosti.

Zbog toga linija se posmatra u parametarskom obliku, a formula glasi:

$x \cdot \cos{\theta} + y \cdot \sin{\theta} = \rho$,

gde je:

• $\theta$ - ugao koji zaklapa normala na pravu sa x osom Slika 9
• $\rho$ - rastojanje od koordinantnog početka do prave
• x, y - parametri

Sada, tačka neće predstavljati pravu već sinusoidu Slika 9, a presečne tačke se određuju na isti način kao što je ranije navedeno.

U narednom koraku definiše se parametarski prostor. Za svaku tačku na slici koja je detektovana kao ivica generiše se sinusoidna kriva koja se beleži, a zatim se traže preseci ovih krivih. Parametarski prostor definišu parametri $\rho$ i $\theta$. Određuju se minimalne i maksimalne vrednosti, odnosno opsezi za svaki od ova dva parametra. Zatim se parametarski prostor deli na više ćelija, u skladu sa željenom preciznošću. U sledećem koraku, za svaku tačku sa originalne slike definiše se odgovarajuća prava, nakon čega se za svaku vrednost parametra $\theta$ izračunava odgovarajući parametar $\rho$. Ukoliko za parametar $\theta_a$ odgovara vrednost $\rho_b$, odgovarajuća ćelija u akumulatoru se inkrementira. Ovaj postupak se ponavlja za sve tačke. Cilj je identifikovati ćelije sa najvećim vrednostima, jer linije koje prolaze kroz ove ćelije sadrže najveći broj tačaka.

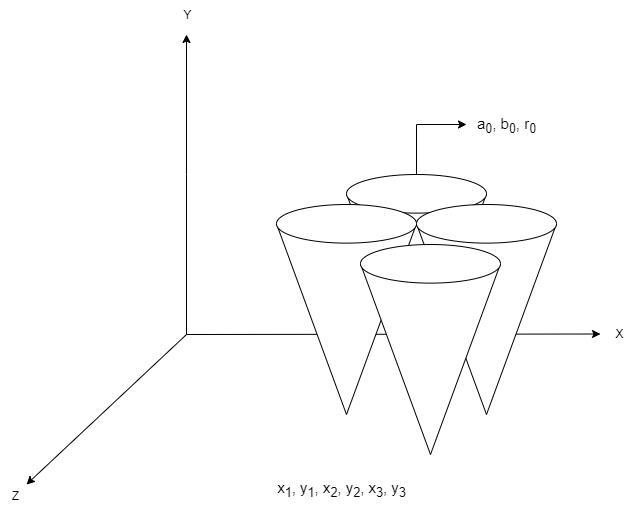
Hafova transformacija za detekciju krugova, kao što je rečeno, identična je transformaciji linije. Kod krugova istih poluprečnika, tačke iz dekartovog se u parametarski sistem slikaju kao kružnice. Dakle, potrebna su samo dva parametra a i b, što sužava pretragu na dve dimenzije. Krug koji se predstavlja jednačinom kružnice

$(x - a)^2 + (y - b)^2 = r^2$ ,

parametarski se predstavlja formulama:

$x = a + r \cdot \cos{\theta}$,

$y = b + r \cdot \sin{\theta}$.

Kod elipsa različitih poluprečnika razlika je u tome što oni zahtevaju tri dimenzije, tj. u parametarski prostor se prenose kao kupasti oblik. Ostatak postupka je isti kao i za LHT.

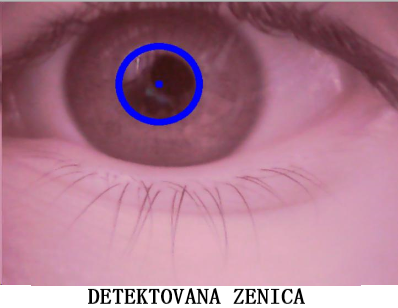
Na slici 11 može se videti detektovana zenica pomoću Hafove transformacije.

3.2.2. Obrada podataka

3.2.2.1. Filter srednje aritmetičke vrednosti (Mean average filter)

Dok konstantno gledamo u jednu tačku dolazi do šuma kao što je treptaj, nenamerno pomeranje oka ili kamere, promena jačine osvetljenja i slično. Ovakve šumove neophodno je otkloniti i u te svrhe koristimo filter srednje aritmetičke vrednosti. Prolazići kroz signal izračunava se aritmetička vrednost prethodnih N merenja koordinata zenice. Ovako izračunate vrednosti se postavlju kao nove koordinate zenice. Na taj način se dobija filtrirano merenje.

Na slici 12 ispod se može videti grafik filtriranog signala, y ose u odnosu na vreme.

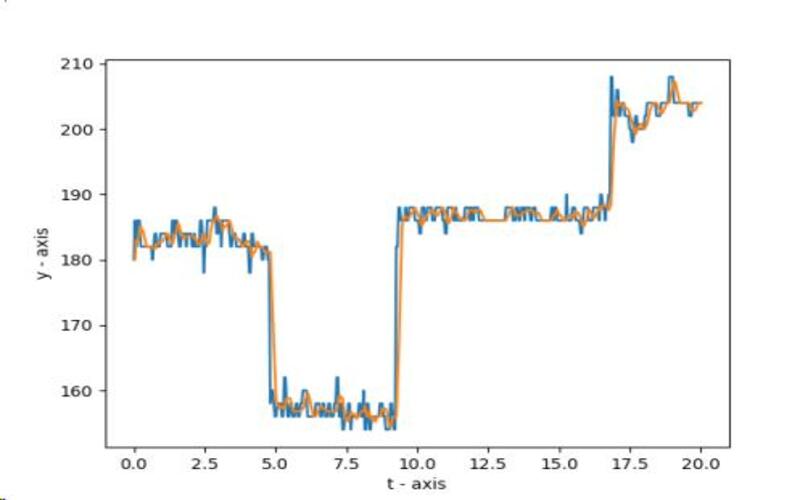
3.2.3. Kalibracija

Nakon detekcije zenice, sprovodi se test kalibracije tokom kojeg se na ekranu prikazuje devet tačaka, u koje se gleda određeni vremenski interval. Tokom eksperimenta prikupljaju se koordinate zenice i koordinate tačke na koju ispitanik trenutno fokusira pogled, čime se formira baza podataka neophodna za dalju analizu.

Izgled ekrana tokom eksperimenta prikazan je na Slici 13. Tokom testa, crvena tačka se pomera nakon definisanog vremenskog perioda, odnosno plave tačke postaju crvene kada je potrebno preusmeriti pogled na njih.

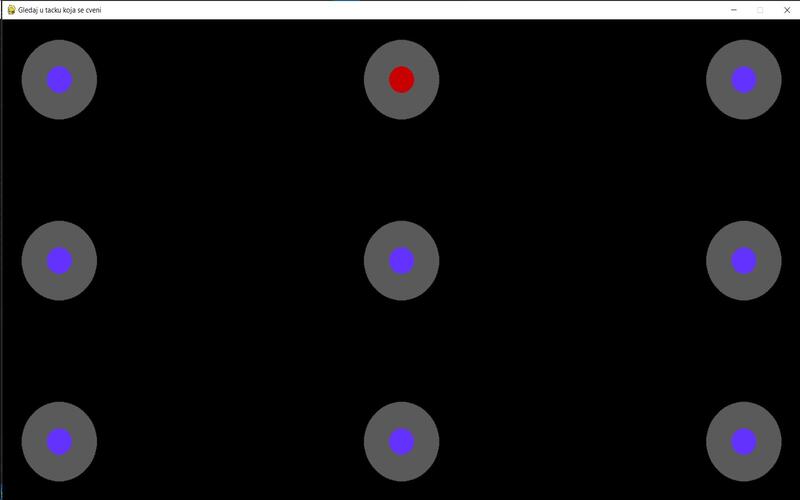
Tokom eksperimenta prikupljamo koordinate zenice i tačke u koju je zenica u trenutku uperena čiji je odnos potrebno pronaći.

3.2.3.1. Linearna regresija

Kako bi se pomoću detekcije zenice kontrolisao objekat na računaru, neophodno je odrediti, na osnovu koordinata centra zenice, u koju tačku na ekranu je oko upereno. Za tu svrhu korišćena je polinomijalna regresija, budući da sistem nije linearan. Sistem nije linearan iz dva razloga: prvi je konveksni oblik oka, koji izaziva nelinarno kretanje zenice, a drugi je činjenica da ravan pogleda (normalna na položaj lica) i ravan ekrana nisu međusobno pod pravim uglom.

Linearna regresija predstavlja modelovanje relacija između jedne ili više zavisnih promenljivih i jedne ili više nezavisnih promenljivih. Model linearne regresije ima oblik:

$ \textbf{Y} = \textbf{X} \cdot b $

gde je:

• $Y$ vektor izmerenih vrednosti (u ovom slučaju koordinate pogleda na ekranu) odnosno zavisna promenljiva

• $X$ vektor ulazne promenljive (u ovom slučaju koordinate zenice oka) odnosno nezavisna promenljiva

• $b$ vektor koificijenta modela

Optimalni vektor parametara $b$ dobija se iz formule za pseudo inverziju koja glasi:

$b = (X^T \cdot X)^{-1} \cdot Y \cdot X^{T}$

gde je:

• $X$ matrica koordinata zence oka

• $Y$ matrica koordinata tačaka na ekranu u koje je predviđeno da se gleda tokom prethodno pomentuog eksperimenta

Ove matrice se dobijaju iz baze podataka generisane tokom prethodno pomenute kalibracije. Dobijen vektor koejficijenta modela $b$ se koristi za izračunavanje koordinta tačaka na ekranu u koje je zenica uperena. Ovako dobijen vektor koeficijenta $b$ nije deltvoran. Konveksni oblik oka izaziva nelinarno kretanje zenice i ugao između ravni pogleda i ravni ekrana nije normalan zbog čega je potrebno koristiti polinomialnu regresiju.

3.2.3.2. Polinomialna regresija

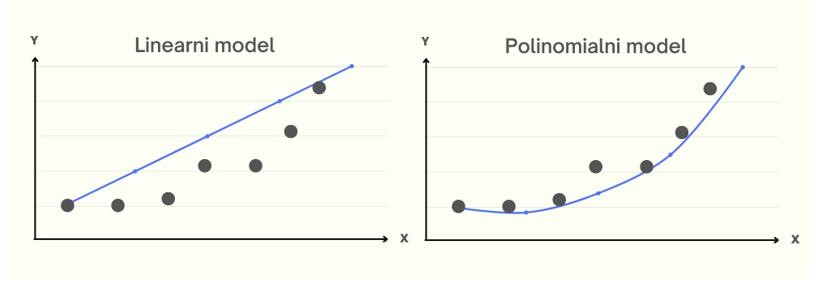
Poliomilna regresija je specijalan slučaj višestruke linearne regresije gde se modeluje veza između zavisne i nezavisne promenljive, u ovom slučaju, između koordinata zenice oka i koordinate pogleda na ekranu, kao polinom n-tog stepena. U ovom slučaju, nema linearne korelacije između promenljivih (slika 14.1), pa se radi veće preciznosti primenjuje poliomilna regresija (slika 14.2).

Za razliku od linearne regresije, kod polinomialne regresije se nezavisna promenljiva x stepenuje stepenom regresije n i zbog toga se dobija bolja korelacija između promenjljivih.

Formula polinomialne regresije glasi:

$y= b_0+b_1 \cdot x_1+ b_2 \cdot x_1^2 + … + b_n \cdot x_1^n$

gde su:

b - koeficijenti regresije

n - stepen regresije (u slučaju ovog rada $n = 3$)

Kako bi izračunali optimalan koeficijent regresije, neophodno je da se polinomialna regresija svede na lineanrnu i nakon toga korišćenjem pseudo inverzije izračuna optimalan koeficijent $b$. Polinomialnu regresiju se svodi na linearnu regresiju tako što se konstruiše matricu $X$:

$\begin{bmatrix} 1 & x_1 & x_1^2 & … & x_1^n \ 1 & x_2 & x_2^2 & … & x_2^n \ . & . & . & . & . \ . & . & . & . & . \ . & . & . & . & . \ 1 & x_m & x_m^2 & … & x_m^n \end{bmatrix}$

U ovoj matrici $n$ predstavlja stepen polinomialne regresije. Ovakvu matricu ćemo iskoristiti u formuli za pseudo inverziju i na taj način dobiti optimalni koeficijent regresije $b$.

Formula za pseudo inverziju: $b = (X^T \cdot X)^{-1} \cdot Y \cdot X^{T}$

4. Rezultati i istraživanja

Model dobijen poliomilnom regresijom je validiran ponovnim snimanjem, ali ovog puta su dobijene predviđen koordinate tačke na ekranu. Na kraju, dobijena je tabela u kojoj, u odnosu na koordinate tačke na ekranu (x, y), se mogu videti pomerenost estimacije i standardna devijacija rasipanja (σx, σy). Rezultati sa jednim snimanjem imaja prosečan pomeraj 121.6 piksela i prosečne standardne devijacije raspipanja σx = 43.48 i σy = 43.13.

X	Y	pomeraj	σx	σy
100	100	133.06	39.53	57.59
700	100	162.63	63.66	13.31
1300	100	143.28	1.07	2.18
100	400	171.49	41.3	98.29
700	100	110.9	51.82	26.37
1300	400	140.46	32.69	50.97
700	100	105.11	59.04	78.9
700	700	20.02	67.81	8.08
1300	700	107.48	34.37	52.48

Na slici 15 prikazana je početna stranica jednog PC računara. Crvena kružnica na slici ima poluprečnik od 121,6 piksela, što predstavlja prosečni pomeraj kursora ovog sistema. Prilikom pokušaja pritiska crvenog kursora, kontrolisanog ovim modelom, može biti pritisnuta neka od tačaka unutar prikazane kružnice. Sa ovakvim prosečnim pomerajem, preciznost kursora je ograničena.

Kako bi se ispitala relevantnost modela, potrebno je izvršiti veći broj snimanja, a za poboljšanje rezultata potrebno je promeniti uslove snimanja. Predlaže se dodavanje IR dioda na 3D držač veb kamere, korišćenje crvenog i plavog filtera za veb kameru, kao i fiksiranje glave tokom snimanja radi smanjenja šuma. Pretpostavlja se da će ovakve izmene doprineti povećanju preciznosti modela.

5. Zaključak

Za testiranje modela korišćen je ispitanik čijom je akvizicijom podataka ostvarena eksperimentalna baza. Problemi su se javljali usled približavanja ili udaljavanja tela od ekrana, kao i promena položaja glave tokom prikupljanja podataka. Pomeraње glave utiče na kalibraciju, jer u tom slučaju koordinate tačke na koju se gleda nisu iste kao na početku eksperimenta. Kako bi se ovi problemi sveli na minimum, preporučuje se izrada čvrstog stalka koji će potpuno imobilisati glavu i obezbediti stabilan oslonac. Očekivani rezultat bio bi usklađivanje koordinata zenice oka sa koordinatama tačke na ekranu, odnosno jasno definisana putanja zenice tokom procesa testiranja (videti Sliku 16).

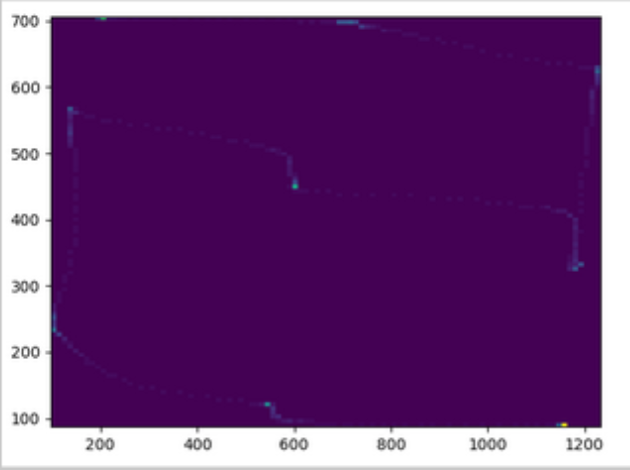
Na dobijenim rezultatima vidi se sledeće - putanja oka prikazana na ekranu nije ista kao putanja kojom je ispitanik pomerao oči.

Za postizanje veće preciznosti rezultata neophodno je sprovesti dodatna testiranja i prikupiti podatke od većeg broja ispitanika. Pored toga, uslovi u kojima su prethodna testiranja realizovana nisu bili optimalni. Promene u osvetljenju izazivaju refleksije u očima, što negativno utiče na tačnost detekcije zenice i generiše šumove prilikom pomeranja oka. Da bi se ovaj problem umanjio, predlaže se implementacija IR dioda na naočare, čime bi se obezbedilo uniformno osvetljenje. Takvo rešenje bi doprinelo značajnom smanjenju šuma u signalima i poboljšanju kvaliteta dobijenih podataka. U daljim fazama istraživanja planira se implementacija navedenih tehničkih izmena, kao i izvođenje dodatnih snimanja radi validacije modela.

6. Literatura