Robot valjak

Autori:

Filip Bajraktari, učenik IV razreda Matematičke gimnazije u Beogradu

Nikola Ristanović, učenik IV razreda Pete begradske gimnazije u Beogradu

Mentori:

Đorđe Marjanović, diplomirani inženjer elektrotehnike i računarstva, PFE

Bojan Roško, diplomirani inženjer elektrotehnike i računarstva, PFE

Danilo Tonić, Elektrotehnički fakulteta u Beogradu

Apstrakt

Tema rada je matematička analiza sfernog robota kao i fizička implementacija njene 2D verzije. Koristeći pravila Lagranžove mehanike izvedene su jednačine kretanja sistema. Te jednačine opisuje kretanje klatna valjka kao i kretanje samog robota. Na osnovu tih jednačina izvedene su odgovarajuće transfer funkcije a zatim konstruisani PID kontroleri. U radu su kompjuterski simulirana tri PID kontrolera. Prvi PID kontroler odžava konstantan ugao inklinacije klatna u odnosu na zemlju. Drugi PID kontroler održava konstantnu ugaonu brzinu valjka. Poslednji PID kontroler održava konstantan ugaoni pređeni put valjka. Napravljen je fizički model robota u kome je implementiran PID koji kontroliše ugao inklinacije robota. Pomoću IMU-a su dobijeni neobrađeni podaci sa žiroskopa i akcelerometra, koji nakon obrade i komplementacije daju ugao inkilnacije klatna. Uz ugao inklinacije i podatke sa obrtnog enkodera se izračunava ubrazanje, brzina i pređeni put robota.

Abstract

The paper’s topic is the mathematical analysis of the spherical robot and physical implementation of its 2D version. Using the rules of Lagrangian mechanics, the equations of motion of the system were derived. These equations describe the movement of the robot’s pendulum as well as the movement of the robot itself. Based on these equations, the appropriate transfer functions were derived, and then the PID controllers were constructed. Three PID controllers are computer simulated in the paper. The first PID controller produces a constant angle of inclination of the pendulum relative to the ground. The second PID controller maintains a constant angular velocity of the robot. The final PID controller maintains a constant angular distance traveled by the robot. A physical model of the robot was created in which the PID that controls the angle of inclination of the robot was implemented. Using the IMU, raw data from the gyroscope and accelerometer were obtained, which after processing and complementation give the angle of inclination of the robot’s pendulum. With the angle of inclination and the data from the rotary encoder, the rotation, speed and distance traveled by the robot are calculated.

1. Uvod

Sferni robot ili robot u obliku lopte je mobilni robot sa sfernim spoljašnjim oblikom. Pokretanje robota se obično izvodi promenom centra mase robota i takav pogonski sistem se naziva sistem pokretnog klatna. Sferni roboti imaju aplikacije u nadzoru, patroliranju i istraživanju terena koji nebezbedan po čoveka. Sferni roboti mogu da rade kao autonomni roboti ili kao daljinski kontrolisani roboti. U skoro svim svernim robotima, komunikacija između unutrašnje pogonske jedinice i eksterne kontrolne jedinice je bežična zbog mobilnosti i zatvorene prirode sferne ljuske. Ideja je bila da se pomoću klatna koje uvek teži da se vrati u stabilan položaj konstruiše robot širokih primena. Takođe, zbog oblika robota sve vitalne komponente se sadržane unutar konture, čineći robota izdržljivijim i jednostavnijim za popravku. Konstrukcija robota ga čini pogodnim za nošenje senzora koji mogu da mere uslove okoline bez velikog izlaganja okruženju.

2. Aparatura i metoda

2.1. Dinamika sistema

Postoje dve vrste sfernih robota koje se razlikuju po načinu konvertovanja električne energije koju motor dobija iz baterije u mehaničku energiju koja dovodi do kretanja robota¹. Prva vrsta robota su sferni roboti sa unutrašnjim pogonskim sistemom (Inside Driving Unit). Takvi roboti u sebi sadrže uglavnom pogonske točkove koji zahvaljujući sili trenja sa unutrašnje strane proizvode moment sile, ili spreg sila ukoliko postoji više takvih pogonskih točkova, što dovodi do rotacije konture i pokretanje robota. S druge strane, postoje sferni roboti koji konvertuju potencijalnu energiju gravitacije u kinetičku energiju rotacije. Takvi roboti izvode njihov centar mase iz ravnotežnog položaja usled čega se javlja moment sile gravitacije na klatno koja teži da klatno vrati u prvobitan položaj. Zbog nedovoljno jake sile trenja između robota i podloge robot počinje da se kreće. U robotu valjku, 2D verziji sfernog robota, je implementirana druga metoda kojom se pomoću elektromotornog pogona klatno valjka izvodi iz ravnotežnog položaja i na taj način pokreće robot. U slučaju robota valjka klatno predstavlja skup komponenti (mikrokontroleri, baterije i ostala elektronika) koje se nalazi ispod ose simetrije valjka.

2.1.1. Horizontalno kretanje

Pre nego što se krene na pravljenje bilo kog hardverskog projekta neophodno je temeljno razumeti mehaniku sistema kako bi mogao da se simulira realni sistem na računaru i na taj način olakša projektovanje i programiranje hardvera. Grana fizike koja se bavi proučavanjem mehanike složenih fizičkih sistema se naziva Lagranžova mehanika. Ona nam služi da složene fizičke sisteme predstavimo matematički isključivo pomoću energija datog sistema. Potencijalne, kinetičke i rotacione kinetičke energije tela i klatna valjka su date sledećim izrazima:

$$U_1 = 0$$
$$U_2 = -M_2gd\cos(\theta _ 1 + \theta _ 2)$$
$$K_1 = \frac{1}{2}M_1(r\omega _ 1)^2$$
$$K_2 = \frac{1}{2}M_2((r\omega _ 1 - d\cos(\theta _ 1 + \theta _ 2)(\omega _ 1 + \omega _ 2))^2 + (d\sin(\theta _ 1 + \theta _ 2)(\omega _ 1 + \omega _ 2))^2)$$
$$T_1 = \frac{1}{2}J_1(\omega _ 1)^2$$
$$T_2 = \frac{1}{2}J_1(\omega _ 1 + \omega _ 2)^2$$

Za razliku od klasične Njutnove mehanike za Lagranžovu mehaniku je potrebno definisati odgovarajući Lagranžijan, koji se definiše kao razlika kinetičikih energija i potencijalnih energija:

$$L = K_1 + K_2 + T_1 + T_2 - U_1 - U_2$$

Iskoristivši Ojler-Lagranžovu jednačinu na dva sistema, klatno i valjak,

$$\frac{d}{dt}\left(\frac{\partial L}{\partial \omega _ 1}\right)\ -\ \frac{\partial L}{\partial \theta _ 1}\ = \ -T + T_f$$ $$\frac{d}{dt}\left(\frac{\partial L}{\partial \omega _ 2}\right)\ -\ \frac{\partial L}{\partial \theta _ 2}\ = \ T$$

dobijaju se sledeće jednačine kojima je u potpunosti opisana dinamika sistema:

$$-T + T_f\ =\ \alpha_1(J_1 + J_2 + M_1r^2 + M_2r^2 + M_2d^2 - 2M_2rd)\ +\ \alpha_2(J_2 - M_2rd + M_2d^2)\ +\ M_2gd(\theta_1 + \theta_2)$$ $$T\ =\ \alpha_1(J_1 - M_2rd + M_2d^2) + \alpha_2(J_2 + M_2d^2) + M_2gd(\theta_1 + \theta_2)$$

gde su iskorišćene aproksimacije za male uglove i male ugaone brzine. Ukoliko važi $$\theta_1 + \theta_2 \ll 1 \ \ ,\ \ \omega_1 + \omega_2 \ll 1$$ mogu se primeniti sledeće aproksimacije:

• $\sin(\theta_1 + \theta_2) \approx \theta_1 + \theta_2$
• $\cos(\theta_1 + \theta_2) \approx 1$
• $\omega_1 + \omega_2 \approx 0$.

2.2. Modelovanje robota

Kako bi se postigao bolji uvid u to kako će se robot ponašati, ključan korak ovog rada je kompjutersko modelovanje robota, odnosno simulacije. Pored samog 3D modela, potrebno je bilo napraviti i niz programa (kompjuterskih simulacija) koji imaju za ulogu da analitički kao i grafički predstave kako bi se robot valjak ponašao pod uticajem različith pobuda i na taj način izbegnu potencijalne greške koje možda ne bi mogle tako lako da se predvide.

2.2.1. Transfer funkcije

Transfer funkcija (ili funkcija prenosa) predstavlja odnos između ulaznog i izlaznog signala upravljačkog sistema, za sve moguće ulazne vrednosti. Za bilo koji kontrolni sistem postoji referentni ulaz ili pobuda koji prolazi kroz transfer funkciju kako bi se proizveo (simulirao) odziv sistema na odgovarajuću pobudu.

Transfer funkcija je definisana kao Laplasova transformacija izlazne promenljive i Laplasove transformacije ulazne promenljive pod pretpostavkom da su svi početni uslovi jednaki nuli. $$G(s)\ =\ \frac{C(s)}{R(s)}$$ Način na koji se formira transfer funkcija kontrolnog sistema je sledeća:

1. Formiraju se jednačine sistema;
2. Uzimaju se Laplasove transformacije jednačina, pretpostavljajući da su početni uslovi jednaki nuli;
3. Određuju se ulazi i izlazi sistema;
4. Na kraju, odgovrajući odnos Laplasove transformacije izlaza i ulaza predstavlja željenu transfer funkciju.

Takođe, važno je naglasiti da izlaz i ulaz nekog sistema ne moraju nužno da budu istih fizičkih dimenzija. Na primer, DC motori se pokreću kada se na njihov ulaz dovede konstantan napon, a kao izlaz sistema može da se prati broj obrtaja motora. Merna jedinica za dati primer bi bila $\ \frac{obrtaj\ po\ sekundi}{\ \ \ napon\ motora}$.

U radu se kao pobuda sistema koristio isključivo napon. To bi značilo da je smanjenje ili povećanje ugaone brzine robota prouzrokovano smanjenju ili povećanju referentnog napona na ulazu motora. Kako bi se znalo na koji način treba implementirati odogovarajuće kontrolere potrebno je analizirati stabilnost odgovarajućih transfer funkcija karakterističnih za datog robota, gde kontroler predstavlja sistem koji nezavisno može da održava unete referentne vrednosti zadate od strane korisnika. Na primer, ukoliko bi korisnik želeo da se robot kreće konstantnom ugaonom brzinom $\omega$, kontroler treba samostalno da podešava napon na motoru tako da se ugaona brzina $\omega$ održava konstantnom.

Prva transfer funkcija koja je analizirana u radu je transfer funkcija ugaone brzine robota u zavisnosti od ulaznog napona.

$$\dfrac{\Omega_1}{V} = \dfrac{\ \ \ \ \ \ \ \ \ \ A + Bs^2}{C + Ds + Es^2 + Fs^3}$$
$A = -2dgK_tM_2$
$B = K_t(-2J_2 + d(-2d+r)M_2)$
$C = dgRT_vM_2 - 2dgK_eK_tM_2$
$D = -T_vK_eK_t + dgRJ_1M_2 + dgr^2RM_1M_2 + dgr^2RM_2^2$
$E = RT_vJ_2 - 2J_2K_eK_t + d^2RT_vM_2 - K_eK_t(J_1 + r^2M_1 + (2d^2 - 3dr + r^2)M_2)$
$F = d^2RJ_1M_2 + d^2r^2RM_1M_2 + RJ_2(J_1 + r^2(M_1 + M_2))$

Druga transfer funkcija koja je analizirana u radu je transfer funkcija ugaone brzine klatna u odnosu na osovinu valjka u zavisnosti od ulaznog napona.

$$\dfrac{\Omega_2}{V} = \dfrac{\ \ \ \ \ \ G + Fs + Es^2}{A + Bs + Cs^2 + Ds^3}$$
$A = dgRT_vM_2 - 2dgK_eK_tM_2$
$B = -T_vK_eK_t + dgRJ_1M_2 + dgr^2RM_1M_2 + dgr^2RM_2^2$
$C = RT_vJ_2 + d^2RT_vM_2 - K_eK_t(J_1 + 2J_2 + r^2M_1 + (2dd - 3dr + r^2)M_2)$
$D = RJ_1J_2 + d^2RJ_1M_2 + d^2r^2RM_1M_2 + r^2RJ_2(M_1 + M_2)$
$E = K_t(J_1 + 2J_2 + r^2M_1 + (2d^2 - 3dr + r^2)M_2)$
$F = K_tT_v$

Koristeći prethodne dve definisane funkcije mogu se izvesti dve nove transfer funkcije za koje važi da su dobijene diferenciranjem polaznih transfer funkcija: transfer funkcija ugaonog pređenog puta robota u zavisnosti od napona na ulazu motora i transfer funkcija ugla klatna u odnosu na osovinu valjka u zavisnosti od ulaznog napona. Treća, i poslednja, transfer funkcija predstavlja zavisnost ugla inklinacije klatna u odnosu na podlogu u zavisnosti od napona motora i dobija se kao paralelna veza prethodne dve transfer funkcije.

2.2.2. PID simulacije

U oblasti automatike postoji niz algoritama (kontrolera) koji imaju za cilj neki vid stabilizacije. To može da bude stabilizacija oko položaja labilne ravnoteže kao što je to slučaj sa problemom inverznog klatna² gde treba da se stabilizuje matematičko klatno u položaju labilne ravnoteže, ili stabilizacija u nekom proizvoljnom položaju koji nalaže zadati problem. Jedan od algoritama koji se pokazao korisnim u praksi je PID kontroler čije su najveće prednosti brza i precizna stabilizacija.

Kako bi se razumeo PID kontroler potrebno je definisati određene termine. Željena vrednost je obično vrednost koju unosi korisnik. Na primer, za sistem za grejanje bi to bila željena temperatura prostorije. Izlaz je kontrolisana vrednost PID kontrolera, tj. izlaz može da bude bilo šta na šta možemo direktno da delujemo a šta neposredno utiče na promenu vredsnoti koju želimo da kontrolišemo. U primeru sa grejačem, uticalo bi se na snagu grejača što bi direktno uticalo na temperaturu prostorije. Greška je vrednost koju koristi PID kontroler da bi odredio na koji način je potrebno manipulisati izlazom kako bi se dostigla željena vrednost. Greška se računa kao razlika željene vrednosti i trenutne vrednosti sistema.

Matematika PID kontrolera

Teorijski posmatrano, transfer funkcije i PID kontroleri su definisani na kontinualnom domenu, tj. definisane su na način koji je nama blizak. Za svaki trenutak u vremenu možemo tačno odrediti vrednost izlaza transfer funkcije. Takva interpretacija nam odgovara ukoliko želimo da ispitujemo osobine same transfer funkcije, ali ukoliko želimo da u realnom svetu implementiramo takav model potrebna nam je transfer funkcija definisana na diskretnom domenu. U tom slučaju znamo tačan izlaz sistema ali na svakih dt sekundi. Prvi razlog zbog kojeg se uvodi ovakav model je taj što bi bilo nemoguće predstaviti beskonačno mnogo vredsnoti kompjuterski, a drugi razlog je taj što je odabir vremenskog intervala dt ograničen odozdo brzinom učitavanja vrednosti sa perifernih uređaja (senzora) i brzinom izvršavanja programa. Transfer funkcija PID kontrolera u kontinualnom domenu je predstavljena sledećim izrazom:

$$C(s) = K_p + \dfrac{K_i}{\ s} + K_ds$$

$K_p$ - proporcionalni koeficijent
$K_i$ - integralni koeficijent
$K_d$ - diferencijalni koeficijent

U tabeli ispod se može videti kako svaki koeficijent utiče na karakteristike PID kontrolera:

PID	RISE TIME	OVERSHOOT	SETTLING TIME	STEADY-STATE ERROR
$\ \ \ \ K_p$	Smanjuje	Povećava	Male promene	Smanjuje
$\ \ \ \ K_p$	Smanjuje	Povećava	Povećava	Smanjuje
$\ \ \ \ K_p$	Male promene	Smanjuje	Smanjuje	Nema promena

Kao i svaku drugu transfer funkciju, PID kontroler možemo diskretizovati koristeći razne metode. Metoda koja je korišćena u ovom radu je Zero-order hold (ZOH metoda), implementirana u biblioteci Python Control Systems Library³.

U radu su simulirana tri PID kontrolera. Prvi PID kontroler odžava konstantan ugao inklinacije klatna u odnosu na zemlju. Drugi PID kontroler održava konstantnu ugaonu brzinu valjka. Poslednji PID kontroler održava konstantan ugaoni pređeni put valjka. Sva tri PID kontrolera mogu nezavisno da se implementiraju ali ukoliko izlaz jednog PID kontrolera prosleđujemo sledećem PID kontroleru možemo da postignemo isti efekat samo će sistem u ovom slučaju biti manje oscilatoran što doprinosti brzini stabilizacije (rising time), i grešci stabilizacije (steady state error). Blok dijagram kontrolnog sistema je predstavljen na slici ispod:

2.2.2.1. Diferencijator

Diferencijator je specijalni oblik transfer funkcije koji ima za ulogu da prima ulazni signal a da kao izlaz prosleđuje funkciju koja odgovara prvom izvodu ulaza. Ovde treba naglasiti da je nemoguće napraviti idealni diferencijator već se na ovaj način postiže aproksimacija željenog efekta. Diferencijator je transfer funcija prvog reda sa nulom u nuli koja je okarakterisana frekvencijom odsecanja (cut-off frequency).

$$D(s) = \dfrac{\ \ \ \omega s \ }{s + \omega}$$

Mana ovakve implementacije diferencijatora je postojanje kašnjenja (lag), o čemu treba voditi računa prilikom implementacije realnog sistema. Kašnjenje se može smanjiti povećanjem frekvencije odsecanja ali će se na taj način žrtvovati tačnost izlaznog signala.

2.2.2.2. Komplementarni filter

Ideja iza komplementarnog filtera je da se uzmu spori signali sa akcelerometra i brzi signali sa žiroskopa i na kraju ih spojimo u jedan signal. Akcelerometar je dobar pokazatelj orijentacije u statičkim uslovima, dok je žiroskop dobar pokazatelj nagiba u dinamičkim uslovima. Dakle, ideja je da se signali sa akcelerometra puste kroz low-pass filter a signali sa žiroskopa da se propuste kroz high-pass filter i onda novodobijeni signali iskombinuju. Low-pass filter nam omogućava da propustimo frekvencije ispod zadate odsečne frekvencije, dok nam high-pass filter omogućava da propustimo frekvencije iznad zadate odsečne frekvencije. Na taj način obezbeđujemo da u svakom trenutku ceo signal podleže oba filtera.

3. Hardver

Pod hardverom se podrazumevaju svi vidljivi delovi robota, poput spojeva, mikrokontrolera, senzora, elektromehaničkih uređaja (motora), napajanja i slično. Šema za povezivanje pojedinčanih komponenti je priložena na slici ispod.

3.1. Lista uređaja

1. IMU (Inertial Mesurement Unit)
2. Arduino Nano
3. Bluetooth modul
4. H-Most
5. Regulator napona
6. DC motor
7. Baterija
8. Optički inkrementalni enkoder

3.2 Princip rada

3.2.1. Arduino Nano i HC05

Uređaj koji vrši prikupljanje i obradu podataka i signala sa senzora, kao i generisanjem signala za upravljanje motorom, je Arduino Nano. Ovo je 16-bitni mikrokontroler koji na sebi poseduje Atmega328p čip. Mikrokontroler u sebi sadrži kod za obradu podataka iz bluetooth modula, IMU-a i enkodera, kod za zadavanje napona motora kao i kod sva 3 PID kontrolera.

3.2.2. Bluetooth modul

HC05 Bluetooth modul komunicira pomoću UART-a, omogućavajući bežični prenos podataka. Napaja se pomoću napona od 5 volti sa mikrokontrolera. Iako modul radi na 5V, napon na signalnim pinovima (RX, TX) je ograničen na 3.3V, tako da je obavezna upotreba naponskog razdelnika kao bi se napon signala sa mikrokontrolera (5V) spustio na odgovarajući nivo. Bežični prenos podataka omogućava uvid u trenutno stanje robota i zadavanje napona i ugla kojim se robot pokreće.

3.2.3. (IMU) - MPU6050

MPU6050 je akcelerometar i žiroskop koji se koristi za merenje ugla inklinacije klatna robota. IMU radi na osnovu merenja ubrzanja duž osa akcelerometra i ugaonog ubrzanja oko osa žiroskopa. Pomoću trigonometrije moguće je izračunati trenutni ugao koji IMU zaklapa u odnosu na ravan zemlje. MPU6050 je sa mikrokontrolerom povezan pomoću I2C protokola. Ovaj senzor mikrokontroleru dostavlja podatke sa žiroskopa i akcelerometra pomoću kojih se u softveru izračunava ugao inklinacije koji je neophodan za određivanje ugaone brzine robota i PID kontrolu.

3.2.4. DC motor i L298N H-most

Budući da pinovi mikrokontrlera nemaju snagu da pokrenu motor, kao pokretač motora se postavlja H-most koji pomoću signala koji dobija od strane mikrokontrolera daje napon motoru motor. Dva signala koje H-most dobija su digitalni signali:

• koji svojim naponom od 0V ili 5V određuje smer, i
• koji koristeći PWM (Pulse Width Modulation) brzim paljenjem i gašenjem kontrolišu napon koji se dovode motoru u opsegu od 0V do 12V.

Koristeći PWM, prividni napon na pinovima mikrokontrolera srazmeran je širini pulsa (Pulse Width) sve dok signal nije potpuno odsutan (0V) ili prisutan (5V). JGA25370 je DC motor koji radi na naponu od 12V i maksimalnoj struji od 2A. Motor u sebi poseduje reduktor koji umanjuje broj obrtaja motora u sekundi ali povećava obrtni momenat gde je broj obrtaja $RPM_{max} = 250$ obrtaja u minutu i obrtni momenat $T = 1.4\ \frac{kg}{cm}$. Ovaj motor je jedina komponenta koja pokreće robota.

3.2.5. Baterija i Stepdown regulator

Napajanje koje se u projektu koristi su četiri redno vezane Samsung 18650-35E litijum-jonske baterije zbog svog kapaciteta od 5000mAh i maksimalne struje od 2A. Baterije se pune eksternim punjačem pomoću balansirajućeg konektora na njima. Napon sa baterije se sprovodi do LM2598 regulatora gde se napon spušta na 12V kako bi dalje mogao da se dovede do H-mosta, budući da je u trenutnoj konfiguraciji njegov napon ograničen na maksimalnih 12V. Potom se struja iz H-mosta pomoću njegovog integrisanog regulatora spušta na 5V i dovodi do mikrokontrolera i ostalih senzora. Napon baterije se meri na mikrokontroleru kroz naponski razdelnik kako bi se napon od 16.8V spustio na 5V što je bezbedno za mikrokontroler. Baterija može da radi oko 3.5h tokom kretanja robota.

3.2.6. Optički inkrementalni enkoder

E38S6G5 je optički enkoder koji se koristi za merenje pređenog puta robota. E38S6G5 ima rezoluciju od 600 pulseva po obrtaju osovine što daje preciznost od 0.6 stepeni ili oko 0.01 radijana. Princip rada optičkog enkodera je da se analizom izlaznih talasa može odrediti da li se enkoder okrenuo u pozitivnom ili negativnom smeru. U konkretnom slučaju na pin 3 mikrokontrolera je povezan prvi od dva izlaza enkodera, gde se prilikom svake rastuće ivice ovog pina mikrokontroler beleži napon na drugom izlazu enkodera. U slučaju da je napon pozitivan mikrokontroler to belezi kao obrt u pozitivnom smeru, a u slučaju da je napon negativan mikrokontroler to beleži kao obrt u negativnom smeru. Kada za svaki ovaj događaj od nekog brojača saberemo ili oduzmemo 1 možemo dobiti ukupni ugao za koji se enkoder zarotirao. Ovime možemo da izračunamo ukupni pređeni put robota i na osnovu toga možemo dobiti trenutnu brzinu.

4. Istraživanje i rezultati

Tokom rada na projektu, uspešno je realizovana hardverska implementacija robota i prikupljeni su podaci o tome kako sistem reaguje na uzastopne odskočne odzive. Tokom istraživanja su izmerena tri odskočna odziva koja redom odgovaraju transfer funkcijama ugla inklinacije klatna u odnosu na podlogu u zavisnosti od napona motora, ugaone brzine klatna u odnosu na podlogu u zavisnosti od ulaznog napona motora i ugaonog pređenog puta robota u zavisnosti od ulaznog napona motora.

Prilikom dizajniranja klatna valjka centar mase korpe i komponenti (baterije, arduino i ostali moduli) se ne nalazi u osnosimetričnoj ravni korpe već je blago izbačen sa strane što dovodi do toga da merenje ugla ne bude centrirano oko nule. Takođe, ovome je potpomogla i činjenica da se na DC motoru nalazi reduktor zbog kog ne postoji prava nula već postoji interval uglova koji mogu biti prava nula. Za male uglove moment zemljine teže na klatno se izjednačava sa momentom sile koju reduktor proizvodi na klatno. Drugim rečima, javalja se mali interval oko prave nule za koje se klatno nalazi u indiferentnoj ravnoteži i u kojoj krajnji položaj zavisi isključivo od početnog impulsa. Ukoliko je veći početni impuls veća je i greška merenja ugla inklinacije. Ovaj fenomen se može predstaviti na grafiku ispod gde se vidi da robot konstantno driftuje u jednu stranu. Za dalji rad na ovom robotu treba da se poravna centar mase sistema kao i da se poveća masa klatna kako bi se smanjio opseg uglova koji mogu biti prava nula i na taj način postići preciznija merenja.

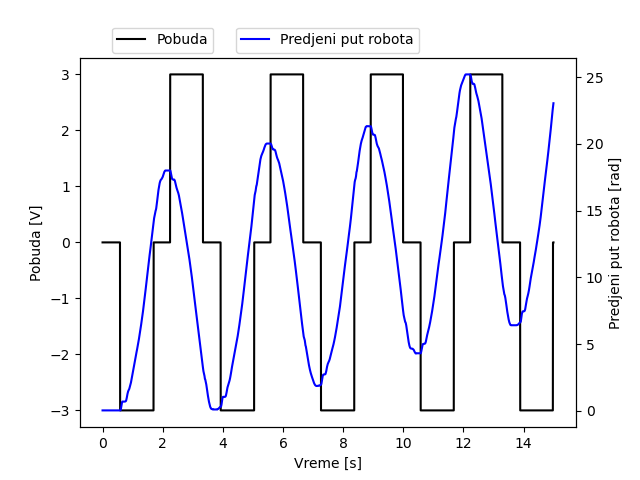
Sledeća dva merenja predstavljaju kako u fizičkom modelu napon na motoru utiče na ugaonu brzinu klatna i ugao inklinacije klatna. Na drugom grafiku se može videti da na početku grafika merenje u stabilnom položaju nije nula. Referentna nula je pomerena za neku vrednost $\Delta\theta$ i razlikuje se od stvarne nule.

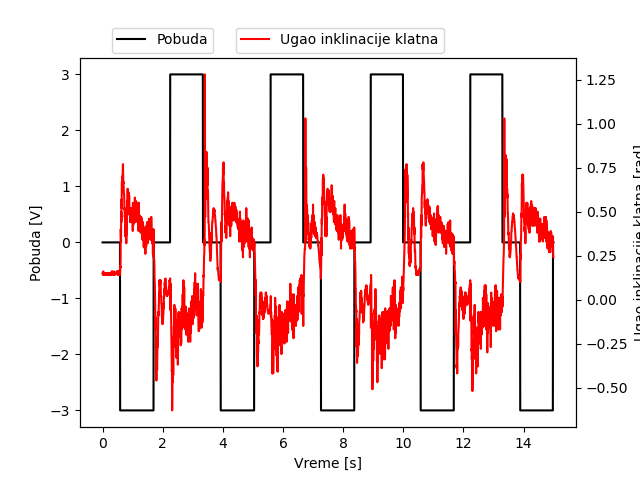
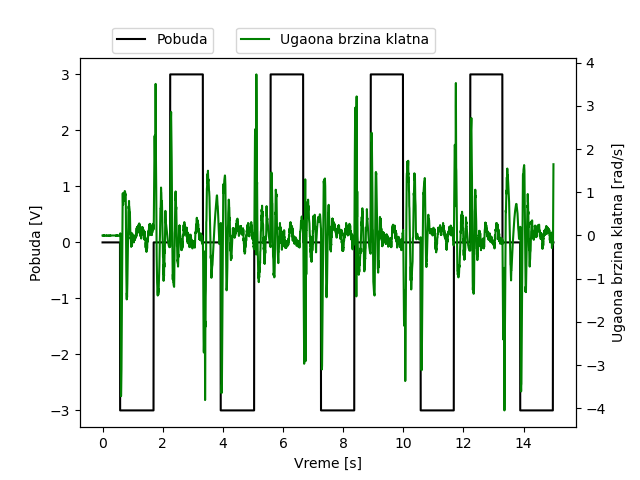
Takođe, na osnovu transfer funkcija se može zaključiti da je sistem oscilatoran, zato su implementirani odgovarajući PID kontroleri. U nastavku se mogu videti grafici stepenastog odziva PID kontrolera dobijeni iz softverskih simulacija:

5. Zaključak

Koristeći pravila Lagranžove mehanike izvedene su jednačine kretanja sistema. Te jednačine opisuje kretanje klatna valjka kao i kretanje samog robota. Jednačine su predstavljene u obliku linearnih diferencijalnih jednačina što dalje omogućava njihovo konvertovanje pomoću Laplasove transformacije u odgovarajuće transfer funkcija. Tako dobijene transfer funkcije nam opisuju kako napon na motoru utiče na ugao inklinacije valjka, ugaonu brzinu valjka i ugaoni pomeraj valjka. Na osnovu transfer funkcija se može zaključiti da je sistem oscilatoran zato su implementirani odgovarajući PID kontroleri koji imaju za ulogu da priguše napomenute oscilacije i u smanje potrebno vreme stabilizacije. U radu su PID kontroleri ulančani i na taj način je omogućeno da viši kontroleri brže i sa manjim oscilacijama stabilizuju sistem nego što bi bio slučaj da nije došlo do ulančavanja PID kontrolera.

Kada je u pitanju hardverska implementacija robota, nakon centriranja težišta klanta dodatnim tegovima, eliminisana je nesimetričnost sistema, što je pomoglo u kontroli robota i ujednačenijem ubrzanju robota u oba smera. Na kontrolu je takođe uticalo i postojanje reduktora na DC motoru koji poseduje mrtav ugao (backlash), što je sve ukupno činilo da umesto jedinstvene referentne nule imamo opseg uglova za koje klatno može da se nađe u indiferentnoj ravnoteži.

Takođe, jedan od ciljeva ovog projekta je bila i numerička identifikacija sistema koja nažalost nije urađena zbog nedostatka vremena kao i gore navedenih problema, ali idalje ostaje kao mogućnost za neki budući rad na ovu ili neku sličnu temu. Pored toga, predlažemo da se u nekom budućem radu da se teg klatna preciznije postavi i izradi od težeg materijala i sa jačim motorom bez reduktora i četkica, kako bi se opseg uglova koji mogu budu referentna nula suzi.

6. Literatura