Simulacija muve

Autori:

Aleksandar Rašković, učenik IV razreda Gimnazije u Subotici

Tadej Ristić, učenik II razreda Računarske gimnazije u Beogradu

Mentori:

Mladen Bašić, Elektrotehnički fakultet u Beogradu

Apstrakt

U radu je predstavljena implementacija fizičke simulacije leta muve u cilju učenja stabilnog letenja primenom veštačke inteligencije. Model muve obuhvata kinematičku i dinamičku simulaciju kretanja u trodimenzionalnom prostoru, sa posebnim akcentom na realističnu rotaciju krila i računanje sile otpora vazduha. Za kontrolu pokreta krila zaduzena je neuronska mreža, čiji su parametri optimizovani genetskim algoritmom. Primenom različitih definicija fitnes funkcije analiziran je uticaj kriterijuma treniranja na stabilnost i efikasnost leta. Eksperimentalni rezultati pokazuju da model uspeva da nauči simulaciju realističnog mahanja krilima, održavanje visine i smanjenje neželjenih bočnih odstupanja.

Abstract

This paper presents an implementation of a physical simulation of a fly’s flight aimed at learning stable flying behavior using artificial intelligence. The fly model includes kinematic and dynamic simulation in three-dimensional space, with emphasis on realistic wing rotation and air drag force calculation. The wing movements are controlled by a neural network whose parameters are optimized using a genetic algorithm. By applying different definitions of the fitness function, the influence of training criteria on flight stability and efficiency was analyzed. Experimental results show that the model successfully learns realistic wing-flapping motion, maintains altitude, and reduces undesired lateral deviations.

1. Uvod

Cilj projekta je implementacija fizičke simulacije letenja muve, u okviru koje se primenom mašinskog učenja (engl. machine learning, ML) može naučiti proces letenja. Za proces učenja korišćena je neuronska mreža u kombinaciji sa genetskim algoritmom. Neuronske mreže i genetski algoritmi su često korišćeni za treniranje simulacija složenih oblika kretanja, poput hodanja ili trčanja. U okviru ovog projekta, razvijen je ML model kojim su kontrolisana krila muve, pri čemu je kretanje postignuto na osnovu simulacije sile otpora vazduha na telo muve.

2. Aparatura i metoda - Fizička simulacija

2.1. Kinematika

Model muve predstavljen je pozicijama karakterističnih tačaka u lokalnom trodimenzionalnom prostoru. Krila su definisana koordinatama tri tačke koje određuju ravan svakog krila. Telo muve modelovano je kao kvadar, pri čemu je svako teme kvadra predstavljeno jednom tačkom. Na model muve pridružen je lokalni koordinatni sistem, kojem su dodeljene pozicija i brzina u globalnom koordinatnom sistemu. Na ovaj lokalni sistem primenjeni su zakoni pravolinijskog i rotacionog promenljivog kretanja. Koordinate tačaka izražene u lokalnom sistemu transformisane su u globalni koordinatni sistem primenom homogenih matrica translacije i rotacije, u cilju vizualizacije u trodimenzionalnom prostoru i izvođenja proračuna u okviru dinamičke simulacije.

Pozicija tačke modela muve u globalnom koordinatnom sistemu dobijena je množenjem vektora lokalnih koordinata odgovarajućom homogenom matricom transformacije $M$. Matrica $M$ formirana je kao proizvod matrice translacije $T$, kojom je definisano pomeranje muve u prostoru, i matrice rotacije $R$, kojom je opisana orijentacija muve u odnosu na koordinatni početak njenog lokalnog koordinatnog sistema:

$$M = T \times R$$

Sličan princip primenjen je i pri rotaciji krila u lokalnom koordinatnom sistemu muve. Za razliku od rotacije oko koordinatnog početka, rotacija krila vršena je oko tačke povezivanja krila sa telom, tj. „zgloba”, koji je korišćen kao centar rotacije. Ova rotacija bila je ograničena unapred definisanim maksimalnim uglom i brzinom pomeranja, čime su sprečene nerealne deformacije i pokreti krila koji nisu fizički ostvarivi u realnom svetu.

2.2. Dinamika

Drugi deo fizičke simulacije obuhvata dinamiku kretanja. Početna ideja bila je simulacija vazduha kao fluida, ali je, usled složenosti implementacije i potrebe za efikasnijim treniranjem neuronske mreže, model pojednostavljen primenom jednačine sile otpora sredine:

$$\textbf{F} = \frac{1}{2}\rho \textbf{v}|\textbf{v}|C_D\textbf{A}$$

gde su:

• $C_D$ — koeficijent sile otpora,
• $A$ — vektor projekcija površine krila na ose globalnog koordinatnog sistema,
• $v$ — vektor brzine krila,
• $\rho$ — gustina vazduha.

Koeficijent otpora zavisi od oblika tela i ugla pod kojim se telo kreće kroz fluid. Umesto tačnog izračunavanja $C_D$ za svaki položaj, primenjena je aproksimacija uvođenjem kosinusa ugla krila u odnosu na pravac kretanja.

Dodatna aproksimacija uvedena je u izračunavanju momenata sila i ugaonog ubrzanja. Umesto dinamičkog određivanja ose rotacije, rotacija je uvek računata oko centra mase muve. Na osnovu rezultantnih sila otpora sredine i gravitacione sile izračunavano je linearno i rotaciono ubrzanje sistema muve. Ta ubrzanja korišćena su za određivanje promene linearne i ugaone brzine u svakom diskretnom vremenskom koraku $dt$.

2.3. Aparatura i metoda - ML

Za kontrolisanje simuliranog leta muve korišćena je neuronska mreža, dok je proces unapređenja mreže vršen primenom genetskog algoritma. Radi integracije sa sistemom simulacije, dodatno je razvijen kod koji koristi navedene komponente kao biblioteke za treniranje modela muve.

Implementacija je organizovana u dva modula:

• network.py — implementacija neuronske mreže,
• geneticAlgo.py — implementacija genetskog algoritma.

Kompletan kod pisan je u programskom jeziku Python 3, pri čemu je za rad mreže korišćena biblioteka NumPy.

Razvijene su dve verzije neuronske mreže:

• Nevektorizovana verzija — implementirana korišćenjem petlji for, neefikasna u pogledu paralelizacije i znatno sporija.
• Vektorizovana verzija — koristi vektorske operacije nad nizovima, što omogućava efikasno izvršavanje na više procesorskih jezgara i niti. Ova verzija značajno ubrzava izvođenje koda.

Dalja razmatranja i prikaz implementacije fokusiraće se isključivo na vektorizovanu verziju neuronske mreže i prateće algoritme prilagođene takvom načinu obrade.

2.3.1. Opis interfejsa za treniranje

Algoritam zahteva od korisnika da inicijalizuje populaciju tipa Population, nad kojom se kasnije poziva funkcija run. Prilikom inicijalizacije populacije, neophodno je proslediti broj jedinki u populaciji, kao i arhitekturu neuronske mreže.

Metoda run zahteva prosleđivanje sledećih parametara:

• fitnes funkcije, koju korisnik sam definiše u skladu sa konkretnim problemom,
• parametara mutacije, uključujući verovatnoću mutacije gena,
• naziva izlaznih fajlova, u koje će biti upisani geni najboljih mreža,
• parametara čuvanja podataka, koji definišu način i učestalost čuvanja rezultata evolucije itd.

Fitnes funkcija predstavlja ključnu komponentu algoritma. Njena uloga je da oceni uspešnost svake jedinke (tj. konkretne neuronske mreže) u izvršavanju zadatka, i na osnovu toga odredi koje će jedinke biti favorizovane u sledećim generacijama. Više detalja o njoj biće dato u nastavku.

Označimo sa $X_{j}^{i}$ j-ti ulazni podatak (input feature) od i-tog seta ulaznih podataka. Onda format matrice ulaznih podataka za funkciju Activate izgleda ovako:

Set 1	Set 2	…	Set m
$X_{1}^{1}$	$X_{1}^{2}$	…	$X_{1}^{m}$
$X_{2}^{0}$	$X_{2}^{2}$	…	$X_{2}^{m}$
…	…	…	…
$X_{n}^{1}$	$X_{n}^{2}$	…	$X_{n}^{m}$

Za svaki poziv funkcije Activate, mreži se prosleđuje $m$ setova ulaznih podataka, pri čemu svaki set sadrži $n$ ulaznih podataka. To implicira da prvi sloj mreže ima $n$ ulaznih neurona. Ulaz se obrađuje paralelno za svih $m$ setova, čime se omogućava vektorska obrada i efikasnije izvršavanje.

Vrednost $m$ može varirati između poziva funkcije Activate, dok vrednost $n$ mora ostati fiksna, u skladu sa arhitekturom mreže koja je unapred definisana.

2.3.2. Neuronska mreža

U okviru ove simulacije, neuronska mreža koristi se za predikciju položaja krila muve u narednom vremenskom koraku, na osnovu trenutnih prostornih parametara tela muve i njenih krila. Za neuronsku mrežu je implementirana propagacija unapred (eng. feedforward). Propagacija unazad (eng. backpropagatoin) nije potrebna jer se mreža trenira genetskim algoritmom.

Za svaki sloj mreže, osim ulaznog, koriste se dve matrice parametara mreže koji se treniraju.Jedna je matrica težina, dok je druga matrica vektor sklonosti (eng. bias). Matrice se čuvaju u rečniku. Slojevi mreže se indeksiraju od nula tako da su parametri u rečniku sačuvani kao $W1, b1, W2, b2, …, Wl-1, bl-1$, ako je $l$ broj slojeva mreže. Obratite pažnju na to da indeksiranje kreće od $0$ i da nulti (ulazni) sloj u mrežu nema parametre.

Označimo sa $W[k]_{ij}$ težinu veze između $i$-tog neurona iz trenutnog ($k$-tog) sloja mreže sa $j$-tim neuronom iz prethodnog ($k-1$) sloja. Onda format za matricu težina $k$-tog sloja neuronske mreže izgleda ovako:

$W[k]_{00}$	$W[k]_{01}$	…	$W[k]_{0m}$
$W[k]_{10}$	$W[k]_{11}$	…	$W[k]_{1m}$
…	…	…	…
$W[k]_{n0}$	$W[k]_{n1}$	…	$W[k]_{nm}$

Dakle, u trenutnom ($k$-tom) sloju neuronske mreže ima ukupno n neurona, odnosno m u prethodnom $(k-1)$ sloju.

Označimo sa $b[k]_{i}$ sklonost tj. bias $i$-tog neurona trenutnog ($k$-tog) sloja neuronske mreže. Onda je format za vektor sklonosti tj. bias-ova $k$-tog sloja neuronske mreže oblika:

$b[k]_{0}$
$b[k]_{1}$
…
$b[k]_{n}$

U trenutnom ($k$-tom) sloju neuronske mreže ima ukupno n neurona. Glavna funkcija u mreži je funkcija za aktivaciju. Njoj se kao parametar prosleđuje matrica ulaznih podataka. Biće korišćena dva pomoćna niza matrica, $A$ i $Z$. Oni će biti dužine $l$ gde je $l$ broj slojeva u mreži. Matrica ulaznih podataka se prepisuje u $A[0]$.

Za svaki sloj $k$, gde $k$ ide od $1$ do $l$ se izvršava jedan korak propagacije unapred, odnosno:

$$ Z[k] = W[k] \times A[k-1] + b[k] $$ $$ A[k] = tanh(Z[k]) $$

Nelinearna funkcija, osim $tanh$, može biti i $sigmoid$ ili $ReLU$. Na kraju je dobijen izlaz mreže, odnosno matrica $A[l]$. Izlaz mreže je istog formata kao i ulazna matrica za mrežu, samo što umesto ulaznih podataka idu izlazni.

2.3.3. Genetski algoritam

Sve informacije o nekoj mreži se nalaze u objektu tipa Genome koji smo implementirali, koji je zapravo njen gen. Objekat gena sadrži razne podatke o mreži u sebi, kao i sve parametre mreže. Pri pravljenju populacije svi parametri dobijaju nasumične vrednosti po gausovoj (normalnoj) raspodeli sa standardnom devijacijom koju možemo da podešavamo.

2.3.3.1. Fitnes funkcija

Kao što je prethodno navedeno, fitnes funkciju korisnik definiše kako bi evaluirao kvalitet svakog genoma u populaciji za konkretni zadatak.

Tokom izvođenja genetskog algoritma, fitnes funkcija se poziva jednom po generaciji i kao argument prima listu genoma. Za svaki genom, korisnik može da:

• Inicijalizuje neuronsku mrežu korišćenjem implementirane funkcije za konverziju genoma u mrežu,
• Pozove funkciju Activate nad dobijenom mrežom, prosleđujući joj ulazne podatke u obliku matrice.

Ulazna matrica treba da bude organizovana tako da svaka kolona predstavlja jedan set ulaznih karakteristika (input features). Ovakav format omogućava paralelnu obradu više ulaza kroz jednu mrežu.

U slučaju ove simulacije, koristi se samo jedna kolona, jer se u svakom pozivu mreža koristi za obradu ulaza koji odgovaraju samo jednoj muvi. Kao rezultat, funkcija Activate vraća vektor izlaznih vrednosti koji se odnosi na taj jedan ulazni set.

Generisanje populacije za novu generaciju gena se sastoji iz 3 faze:

• selekcija,
• ukrštanje,
• mutacija.

2.3.3.2. Faza selekcije

Nakon što se završi fitnes funkcija program bira 10% najboljih gena, poređanih po fitnesu koji im je dodeljen u fitnes funkciji. Oni se smeštaju u niz, nazvan „bazenom za ukrštanje”. Ovi geni će se koristiti za generisanje nove populacije gena.

2.3.3.3. Faza ukrštanja

Novi geni se generišu tako što se nasumično biraju dva „roditelja” iz „bazena za ukrštanje”, zatim se na njima vrši ukrštanje i novodobijeni gen se dodaje na novu populaciju. Proces se ponavlja dok se populacija ne popuni istim brojem gena kao što je bio u prethodnoj generaciji.

Novi gen može biti generisan iz dva roditelja primenom različitih metoda kombinovanja njihovih parametara. U ovoj implementaciji koristi se probabilistički pristup:

• Za svaki pojedinačni element gena, postoji verovatnoća $x$ da će taj element biti preuzet iz gena prvog roditelja, odnosno verovatnoća $1−x$ da će biti preuzet iz gena drugog roditelja.

Vrednost $x$ se definiše kao jedan od parametara koji se prosleđuju funkciji run prilikom izvršavanja genetskog algoritma, i omogućava korisniku da kontroliše stepen kombinovanja roditeljskih osobina u novim jedinkama.

2.3.3.4. Faza mutacije

Nakon faze ukrštanja vrše se nasumične mutacije na svakom od novih gena. Mutacija podrazumeva da se vrednosti na nasumičnim mestima u genu postave na neke nove nasumične vrednosti. Učestalost mutacija u novom genu je takođe jedan od parametara koji se moše proslediti run funkciji.

Ova faza je bitna kako bi održali diverzitet populacije, tj. kako se ne bi cela populacija svela na par sličnih gena i tako stagnirala.

2.3.3.5. Dodatna faza

Umesto da svi geni iz nove populacije budu dobijeni na prethodni način, program 5% najboljih gena iz prošle generacije prepiše bez promena, kako se ne bi desilo da se kroz prethodne faze izgubi dosadašnji napredak.

2.3.4. Čuvanje podataka

Za čuvanje podataka kao što su najbolji gen muve za određene generacije ili cela populacija u nekom trenutku treniranja, korišćena je biblioteka pickle. Ova biblioteka omogućava da u fajlovima sa .pickle ekstenzijom sačuvamo python objekat koji se lako može vratiti u program. Najbolji gen iz neke generacije se čuva kada njegov fitnes postane veći od parametra fitness_treshold, onda program čuva najbolji gen u fajl i povećava fitness_treshold za delta_fitness kako bi čuvao samo fajlove kada algoritam napravi neki pomak. Nakon što se završi treniranje na zadatom broju generacija, program čuva poslednju populaciju. Ovo je bitno ukoliko želimo da treniramo populaciju iz više puta. Omogućava nam menjanje fitnes funkcije i ostalih parametara između dva dela treniranja. Parametri fitness_treshold, delta_fitness i sl. mogu se proslediti run funkciji koju se poziva nad populacijom.

2.3.5. Treniranje muve

Jedan deo veze između genetskog algoritma i fizike je implementiran kodom koji generiše populaciju p od 100 jedinki čija je arhitektura mreže [15, 20, 20, 3]. Ovo znači da u ulaznom sloju u mrežu postoji 15 neurona, u dva skrivena sloja po 20 neurona i u izlaznom sloju postoji 3 neurona. Ulaznih 15 neurona predstavljaju trodimenzionalne vektore pozicije muve, rotacije muve, brzine muve, brzine rotacije muve i rotacije jednog krila. Mreža na izlazu izbacuje novu rotaciju krila u sledećem trenutku. Krila su podešena da se kreću simetrično tako da su dovoljni podaci samo za jedno krilo. Ukoliko se aktivira opcija za nesimetrična krila, bilo bi potrebno 18 ulaznih neurona i 6 izlaznih.

Prvo se pravi populacija sa odabranim karakteristikama i nad njom se poziva funkcija run kojoj se prosledjuju fitnes funkcija, broj generacija, šansa za preuzimanje gena od drugog roditalja umesto prvog u fazi ukrštanja, šansa da se desi mutacija za svaki parametar neuralne mreže u mutation fazi, i slični parametri. Takođe se prosleđuju i parametri vezani za čuvanje fajlova najboljih gena ili celih populacija.

Fitnes funkcija nazvana main prima listu gena kao parametar. Na osnovu te liste generiše listu neuralnih mreža. Za svaku muvu, tj. gen, mreža se prosleđuje funkciji za simulaciju kretanja muve koja vraća podatke o poziciji, rotaciji i ostalim parametrima muve u svakom trenutku simulacije.

Za svaki gen nakon izvršavanja pomenute funkcije računa se fitnes, gde se uzima da je fitnes jednak visini muve u poslednjem trenutku simulacije. Nakon što se ovaj proces izvrši za svaku muvu, funkcija se završava. Zatim se stvaraju nove generacije gena za muve i opet se pokreće fitnes funkcija sa novim genima.

3. Istraživanje i rezultati

Cilj istraživanja je podrazumevao razvoj kontrole leta muve uz maksimizaciju visine njenog položaja duž y-ose.

Kao prvi pristup u proceni performansi neuronskih mreža, fitnes funkcija postavljena je na vrednost prosečne visine muve tokom simulacije, odnosno na prosek y-koordinate njenog položaja. Dužina simulacije ograničena je na 3 sekunde. Za simulacije u trajanju od 1 sekunde, izvršavanje je trajalo značajno kraće od jedne sekunde realnog vremena, što je pozitivno uticalo na ukupnu brzinu treniranja.

Nakon pokretanja koda, primećeno je da je program često neočekivano prekidao izvršavanje. Vizuelnom analizom simulacije utvrđeno je da se visina muve u određenim trenucima naglo i neprirodno menjala, što je moglo da se uoči i na prikazanom grafiku.

Zaključeno je da je problem bio u kontroli krila muve pomoću neuralne mreže svake milisekunde simulacije što je dovelo do toga da muva pokušava da pravi prebrze pokrete koji su mogli da postave određene promenjive na vrednosti koje odgovaraju beskonačnosti zbog kojih bi pri kasnijim proračunima došlo do greške.

Nakon što je podešeno da se krila kontrolišu na svakih 10 milisekundi, problem je rešen. Dobijen je sledeći grafik:

Sa grafika se može zaključiti da je muva uspela da proizvede pokrete koji imitiraju mahanje krilima, međutim, intervali između zamaha su predugi. To dovodi do toga da muva naglo gubi visinu pre nego što ponovo aktivira krila. Ovakvo ponašanje ukazuje na to da mreža nije efikasno naučila povratni pokret krila u položaj iz kog se inicira naredni zamah.

Drugim rečima, mreža ne optimizuje dovoljno fazu vraćanja krila na početni položaj, što rezultira neefikasnim održavanjem visine tokom simulacije.

Nakon što je fitnes izjednačen sa visinom muve po y osi u poslednjem trenutku simulacije, visina koju je buba dostizala je poboljšana za 2-3 puta. Grafik je onda izgledao ovako:

Uočeno je da je kod muve naučeno optimalno vraćanje krila u gornji položaj, bez dodatnog spuštanja.

Nakon svakih $x$ generacija čuvani su svi podaci o položajima muva u datoj generaciji, što je omogućilo rekonstrukciju 3D prikaza celokupne simulacije. Na osnovu ovih prikaza, uočeno je da se muva ne kreće vertikalno već ukoso, odnosno značajno odstupa duž $x$ i $z$ ose.

Kako bi se suzbilo ovo neželjeno bočno kretanje i podstakla stabilna vertikalna putanja, redefinisana je fitnes funkcija:

$ fitness = Y_t - (\frac{1}{T} * \sum_{i = 1}^{T}(X_i)) * \frac{1}{5} - (\frac{1}{T} * \sum_{i = 1}^{T}(Y_i)) * \frac{1}{5}$

• X, Y i Z - nizovi koordinata u svakoj milisekundi simulacije,

• T - vreme trajanja simulacije u milisekundama.

Fitnes je visina muve u poslednjem trenutku od koje se oduzima jedna petina prosečnog odstupanja x i z koordinate muve od 0, jer to nije toliko bitno koliko i visina muve.

Nakon treniranja 50 generacija muva na 3 sekunde dobili smo sledeći grafik koji predstavlja fitnes u odnosu na broj generacija:

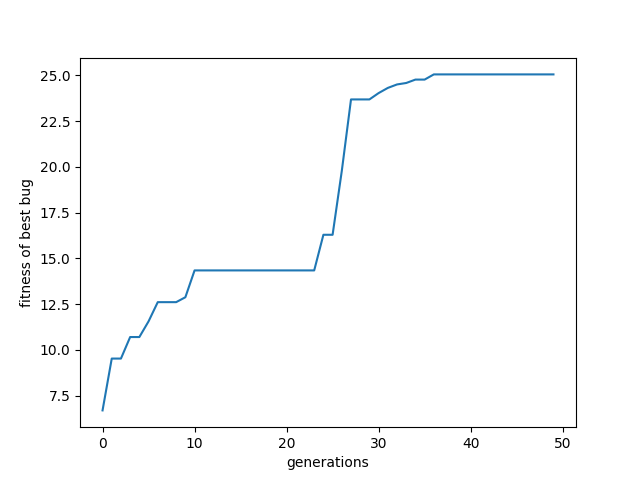
Sledeći grafik predstavlja fitnes u odnosu na broj generacija, nakon treniranja od 1000 generacija:

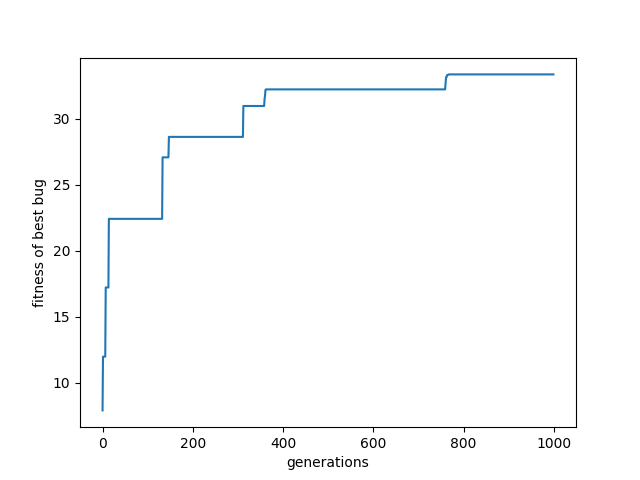
Na kraju je produženo trajanje simulacije na 30 sekundi na kome se veoma lepo vidi muva maše krilima i kako se ne kreće toliko po x i z osama.

Simulacija kinematike se vrši sa vremenskim stepenom od 1ms. Radi preciznije simulacije bržih pokreta moguće je još smanjiti $dt$, ali time se usporava brzina treniranja simulacije.

4. Zaključak

Pokazano je da se ovim pristupom mogu postići rezultati koji su prilično realistični, pri čemu je potvrđeno da je algoritam sposoban da nauči zadato ponašanje na osnovu definisanih uslova.

Ova ideja može se proširiti razvojem kontrolera za upravljanje kretanjem bube, putem kog bi korisniku bilo omogućeno određivanje pravca kretanja. Kretanje bube trebalo bi da se odvija u skladu sa komandama koje zadaje korisnik.

Ovakva funkcionalnost može se ostvariti korišćenjem više neuronskih mreža, treniranih istim algoritmom, ali sa različitim fitnes funkcijama. Neophodno je obučiti jednu mrežu za lebdenje bube u blizini određene tačke, kao i po jednu mrežu za kretanje u sva četiri pravca (odnosno šest pravaca, ukoliko se omogući kretanje i duž y-ose).

Tokom procesa treniranja mogu se koristiti različiti početni parametri, tako da buba ne mora uvek započinjati kretanje iz stanja mirovanja. Na kraju, ovako istrenirane mreže mogu se integrisati u jedinstven kontroler, u kojem bi se, u zavisnosti od korisničke komande, aktivirala odgovarajuća mreža za upravljanje kretanjem bube.